- Published on
Stable Marriage Problem
Table of Contents
The problem of matching the preferences of one group of entities with the preferences of another group of entities is found in many areas. Let’s look into some of them.
College/School Admissions: Students have a list of institutes in order of preference they want to get admitted into. And similarly, these institutes have their own preferences regarding which applications they want to select.
Load Balancing inside a CDN system: A Content Delivery Network (CDN) is a globally distributed group of servers that caches content and delivers it to the users from servers geographically closest to them, resulting in shorter load times. A CDN has a global load balancer that has to map requests to these servers. These requests have a preference list over the servers based on criteria such as lower latency, higher throughput, etc. Similarly, servers also have a preference list over these requests which could be based on factors such as the IP Address of the request.
Organ Donor to Patient Matching: Orgran Donors and Patients need to be matched and their preference list could be built based on their blood type, tissue type, etc.
All these problems and many others can be generalized and can be put under the category of stable marriage problem.
The Stable Marriage Problem
Suppose we have an equal number of men and women and all of them has a list of preference for whom they want to marry. Then Stable Marriage is a matching of men to women such that there exists no man and a woman where they prefer each other more than the partner they are married to.
A blocking pair is a pair of a man and a woman such that both of those prefer each other more than their current partner.
So, we can redefine the Stable Marriage Problem as a matching of men to women such that there exists no blocking pair.
For example:
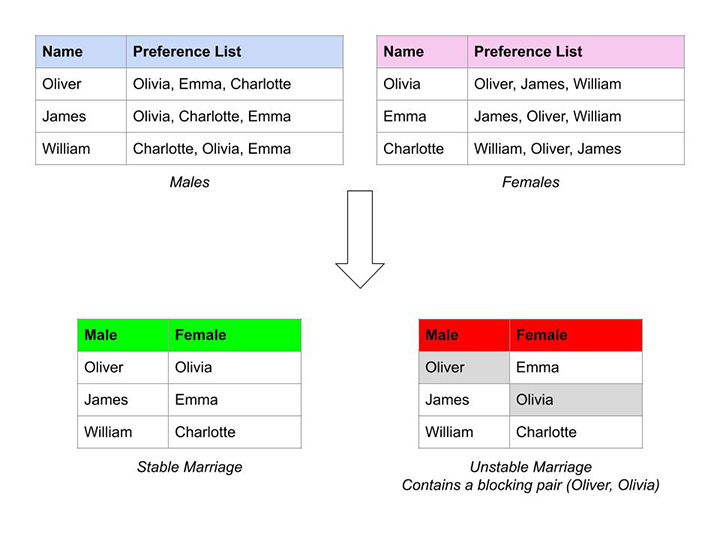
It’s worth noting that the notion of stability accounts for the preferences of all the participants. If and only if there is no blocking pair among all the participants only then we’ll say the marriage is stable.
Gale-Shapley Algorithm
In 1962, David Gale and Lloyd Shapley presented an algorithm that solves SMP. It is also known as the deferred acceptance algorithm.
- The algorithm works in rounds and initially, every participant is free. In each round, every free man proposes to his most preferred woman that he has not already proposed to, and it doesn’t matter whether she is engaged or free.
- The woman accepts the proposal only if she’s free or if she prefers the current man more than the one she’s engaged to. If it’s the latter case then the previous engagement is broken and the man becomes free again.
- The algorithm terminates when everyone is engaged.
This algorithm is said to be man-optimal because each man is married to the most preferred woman he could possibly marry whereas it’s not the case for the women. If we want the marriage to be woman-optimal then we can execute the algorithm with the roles reversed.
public class GaleShapleyAlgorithm
{
public Couples Match(IEnumerable<Entity> males)
{
var couples = new Couples();
while (true)
{
foreach (var male in males)
{
if (couples.IsEngaged(male))
{
continue;
}
var preferredFemale = male.NextPreferred();
if (couples.IsEngaged(preferredFemale))
{
if (preferredFemale.MorePreferred(male, couples.GetPartner(preferredFemale)) == male)
{
couples.BreakEngagement(preferredFemale);
couples.Engage(male, preferredFemale);
}
}
else
{
couples.Engage(male, preferredFemale);
}
}
if (males.All(m => couples.IsEngaged(m)))
{
break;
}
}
return couples;
}
}
Complete source code
You can checkout the complete source code here.
Find Blocking Pair
It might not obvious from the problem but a stable marriage always exists. A woman rejects a proposal only if she’s engaged with a more preferred partner. Now suppose a man keeps on getting rejected by each woman and even the last woman on his list rejected him. That means she’s engaged. But since there are an equal number of men and women and no participant can have more than one partner that means all men are engaged too, which is a contradiction.
But still, if we have to check for a blocking pair then how would we check if it exists or not? Well, there is a simple algorithm that we can use to check for blocking pairs.
For each man, we need to check all the women that he prefers over his partner, if any of those women prefer him over their partner, then we have found a Blocking Pair.
public class BlockingPairFinder
{
public bool Exists(Couples couples, IEnumerable<Entity> males)
{
foreach (var male in males)
{
foreach (var morePreferredFemale in male.MorePreferredList(couples.GetPartner(male)))
{
if (morePreferredFemale.MorePreferred(male, couples.GetPartner(morePreferredFemale)) == male)
{
return true;
}
}
}
return false;
}
}